かぬです.
モンティ・ホール問題について実装したのでメモを残します.
モンティ・ホール問題の詳細については下記をご確認ください.
(かぬが解説するより詳細が載ってるので)
意味や解釈などは追記していけたらと思っています.
私の学習時点でのメモなので,実装内容についての責任を持てません.
ご了承ください.
import random
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
sns.set_style('whitegrid')
#シミュレーションパラメータ
l = [0, 0, 1,]#選択肢,あたりが1として定義
triNum=1000 #一回のシミュレーションの試行回数
sessionNum=10#シミュレーションの繰り返し回数
#changeの時に必ず選択肢を変える,noChangeの時は最初の選択を維持し続ける
states= ['noChange','change']
fig,ax=plt.subplots(1,2,figsize=(10,5))#図の作成
d_c={'change':'red','noChange':'blue'}#図の色指定
# 計算
mean_state,std_state=[],[]
for state in states:
prob_serieses,probs =[],[]
for j in range(sessionNum):
sum_n,prob_series=0,[]
for i in range (triNum):
c1=random.choice(l)
if state=='change':
if c1==0:
c1=1
elif c1==1:
c1=0
sum_n=sum_n+c1
prob_series.append(sum_n/(i+1))
prob_serieses.append(prob_series)
probs.append(sum_n/triNum)
ax[0].plot(prob_series,alpha=0.1,color=d_c[state])
mean_state.append(np.mean(probs))
std_state.append(np.std(probs))
ax[0].plot(np.mean(prob_serieses,axis=0),alpha=1,color=d_c[state],label=state,lw=3)
ax[1].bar([0,1],mean_state,yerr=std_state,ecolor="black", capsize=10,color=['blue','red'],alpha=0.5,tick_label=states)
# 図の書式
ax[0].set_xlabel('Trial Num [-]')
ax[0].legend()
for a in ax:
a.set_ylim(0,1,2)
a.set_ylabel('Probability [-]')
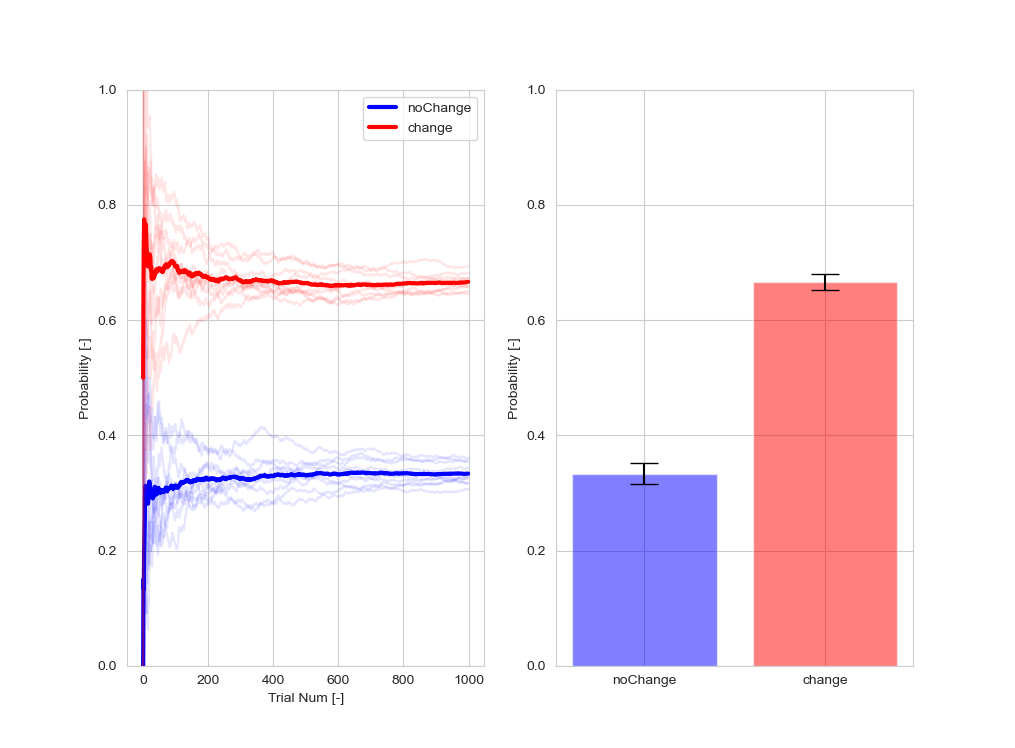
plt.show()実行すると,下記のように変更しなかった場合には1/3,変更した場合には2/3の確率で当たりを引くことができることがわかります.
それでは.


